数的范围

给定一个按照升序排列的长度为 n的整数数组，以及 q 个查询。

对于每个查询，返回一个元素 k 的起始位置和终止位置（位置从 0 开始计数）。

如果数组中不存在该元素，则返回 -1 -1。

输入格式

第一行包含整数 n 和 q，表示数组长度和询问个数。

第二行包含 n 个整数（均在 1∼100001∼10000 范围内），表示完整数组。

接下来 q 行，每行包含一个整数 k，表示一个询问元素。

输出格式

共 q 行，每行包含两个整数，表示所求元素的起始位置和终止位置。

如果数组中不存在该元素，则返回 -1 -1。

数据范围

1≤n≤100000
1≤q≤10000
1≤k≤10000

经典的二分模板题。

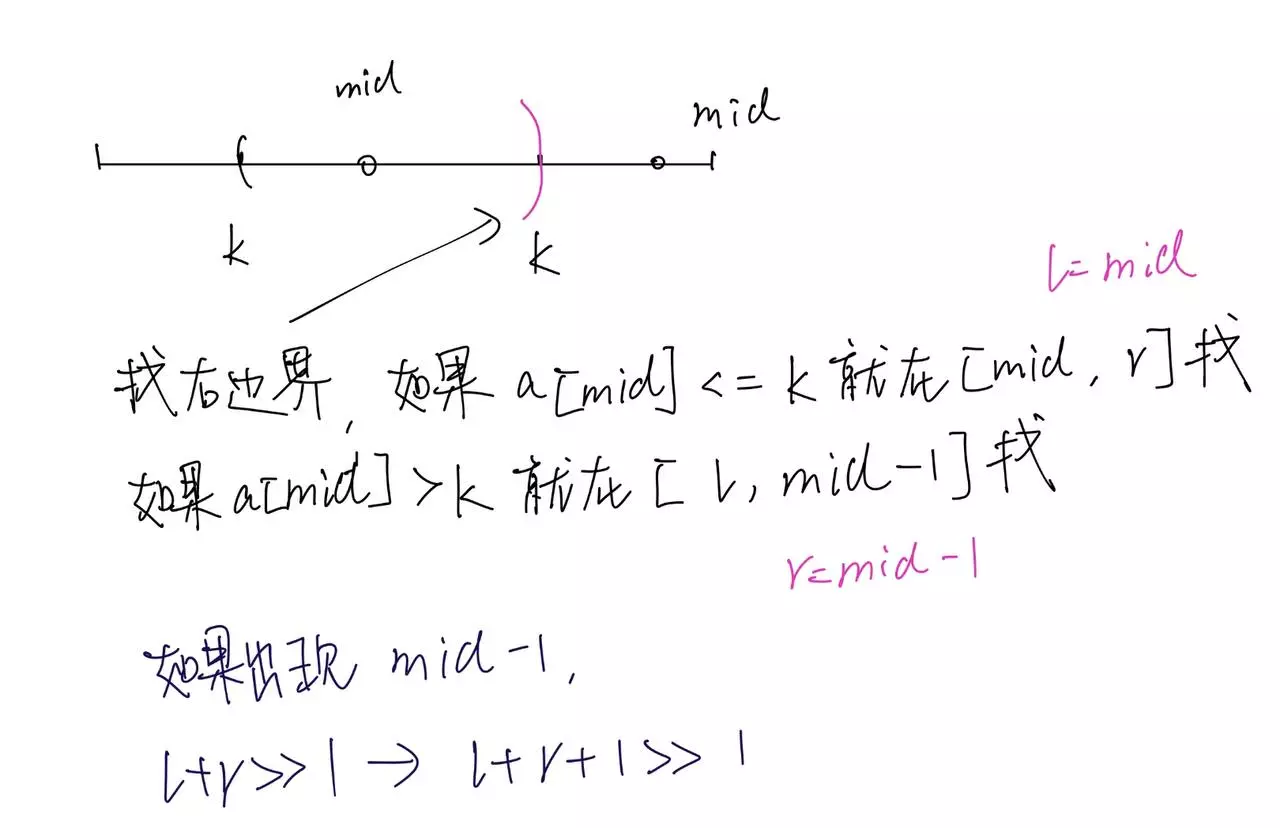
题目要找k的左边界和右边界。

二分

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
#include<iostream>
using namespace std;
const int N = 1e5+10;
int a[N];


int left_bound(int k,int n){
    int l=0,r=n-1;
    while(l<r){
        int mid=l+r>>1;
        if(a[mid]>=k) r=mid;
        else l=mid+1;
    }
    return l;
}

int right_bound(int k,int n){
    int l=0,r=n-1;
    while(l<r){
        int mid=l+r+1>>1;
        if(a[mid]<=k) l=mid;
        else r=mid-1;
    }
    return l;
}

int main(){
    int n,q;
    cin>>n>>q;
    for(int i=0;i<n;i++) cin>>a[i];
    for(int i=0;i<q;i++){
        int k;
        cin>>k;
        int left=left_bound(k,n);
        int right=right_bound(k,n);
        if(a[left]-k) {
            left = -1;
            right= -1;
        }
        cout<<left<<" "<<right<<endl;
    }
    return 0;
}