腐烂的橘子

在给定的 m x n 网格 grid 中，每个单元格可以有以下三个值之一：

  • 值 0 代表空单元格；
  • 值 1 代表新鲜橘子；
  • 值 2 代表腐烂的橘子。

每分钟，腐烂的橘子 周围 4 个方向上相邻 的新鲜橘子都会腐烂。

返回 直到单元格中没有新鲜橘子为止所必须经过的最小分钟数。如果不可能，返回 -1 。

示例 1：

img

1
2
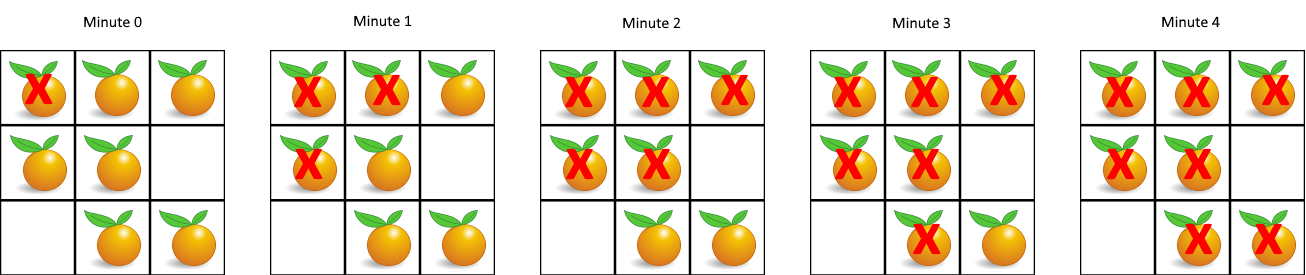
输入：grid = [[2,1,1],[1,1,0],[0,1,1]]
输出：4

示例 2：

1
2
3
输入：grid = [[2,1,1],[0,1,1],[1,0,1]]
输出：-1
解释：左下角的橘子（第 2 行， 第 0 列）永远不会腐烂，因为腐烂只会发生在 4 个方向上。

示例 3：

1
2
3
输入：grid = [[0,2]]
输出：0
解释：因为 0 分钟时已经没有新鲜橘子了，所以答案就是 0 。

提示：

  • m == grid.length
  • n == grid[i].length
  • 1 <= m, n <= 10
  • grid[i][j] 仅为 0、1 或 2

橘子的腐烂过程是一个按层扩散的过程，所以可以用BFS解决。

  1. 初始化：

    • 遍历整个网格，将所有腐烂的橘子（值为 2）的坐标加入队列，作为 BFS 的起点。
    • 统计新鲜橘子（值为 1）的数量，记为 countFresh。

  2. BFS 过程：

    • 从队列中取出当前层的所有腐烂橘子，检查它们的上下左右四个方向。
    • 如果某个方向上有新鲜橘子，则将其腐烂，并将其坐标加入队列，同时减少 countFresh。
    • 每一层 BFS 代表一分钟的腐烂过程。

  3. 终止条件：

    • 如果 BFS 结束后，countFresh 仍然大于 0，说明有新鲜橘子无法被腐烂，返回 -1。
    • 否则，返回 BFS 的层数，即所需的最小分钟数。
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39
    40
    41
    42
    43
    44
    45
    46
    47
    48
    49
    50
    51
    52
    53
    54
    55
    56
    class Solution {

        class Point {
            int x;
            int y;

            public Point(int x, int y) {
                this.x = x;
                this.y = y;
            }
        }

        Point[] queue;
        int l = 0;
        int r = 0;

        public int orangesRotting(int[][] grid) {
            if (grid == null || grid.length == 0)
                return 0;
            int m = grid.length;
            int n = grid[0].length;
            queue = new Point[m * n];
            int freshCount = 0;
            for (int i = 0; i < m; i++) {
                for (int j = 0; j < n; j++) {
                    if (grid[i][j] == 2) {
                        Point point = new Point(i, j);
                        queue[r++] = point;
                    }
                    if (grid[i][j] == 1) {
                        freshCount++;
                    }
                }
            }
            int minutes = 0;
            int[] dx = { 0, 1, 0, -1 };
            int[] dy = { 1, 0, -1, 0 };
            while (l < r && freshCount > 0) {
                int size = r - l;
                minutes++;
                for (int i = 0; i < size; i++) {
                    Point point = queue[l++];
                    for (int d = 0; d < 4; d++) {
                        int x = point.x + dx[d];
                        int y = point.y + dy[d];
                        if (x >= 0 && x < m && y >= 0 && y < n && grid[x][y] == 1) {
                            freshCount--;
                            grid[x][y] = 2;
                            queue[r++] = new Point(x, y);
                        }
                    }
                }
            }
            return freshCount > 0 ? -1 : minutes;
        }
    }