差分矩阵

输入一个 n 行 m 列的整数矩阵，再输入 q 个操作，每个操作包含五个整数 x1,y1,x2,y2,c，其中 (x1,y1) 和 (x2,y2) 表示一个子矩阵的左上角坐标和右下角坐标。

每个操作都要将选中的子矩阵中的每个元素的值加上 c。

请你将进行完所有操作后的矩阵输出。

输入格式

第一行包含整数 n,m,q。

接下来 n行，每行包含 m个整数，表示整数矩阵。

接下来 q行，每行包含 55 个整数 x1,y1,x2,y2,c，表示一个操作。

输出格式

共 n 行，每行 m 个整数，表示所有操作进行完毕后的最终矩阵。

数据范围

1≤n,m≤1000,
1≤q≤100000,
1≤x1≤x2≤n,
1≤y1≤y2≤m,
−1000≤c≤1000,
−1000≤矩阵内元素的值≤1000−1000≤矩阵内元素的值≤1000

输入样例：

1
2
3
4
5
6
7
3 4 3
1 2 2 1
3 2 2 1
1 1 1 1
1 1 2 2 1
1 3 2 3 2
3 1 3 4 1

输出样例：

1
2
3
2 3 4 1
4 3 4 1
2 2 2 2

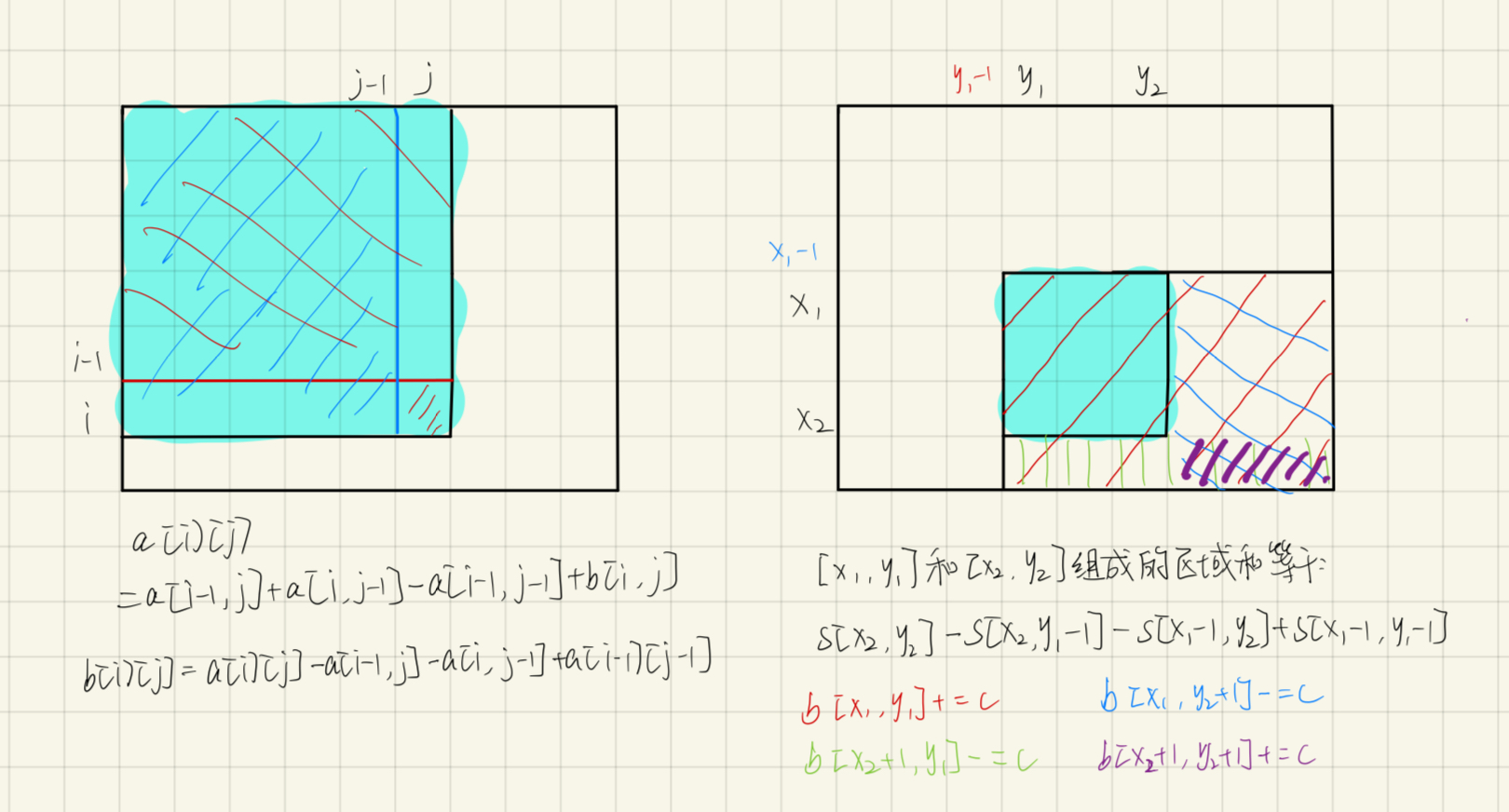
二维版的差分。

同样也是二维版前缀和的逆运算

差分矩阵

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
#include<iostream>
using namespace std;

const int N = 1e3+10;
int a[N][N],b[N][N];

int main(){
    int n,m,q;
    cin>>n>>m>>q;
    for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++)
            cin>>a[i][j];
    for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++)
            b[i][j]=a[i][j]-a[i][j-1]-a[i-1][j]+a[i-1][j-1];
    while(q--){
        int x1,y1,x2,y2,c;
        cin>>x1>>y1>>x2>>y2>>c;
        b[x1][y1]+=c;
        b[x1][y2+1]-=c;
        b[x2+1][y1]-=c;
        b[x2+1][y2+1]+=c;
    }
    for(int i=1;i<=n;i++){
        for(int j=1;j<=m;j++){
            a[i][j]=b[i][j]+a[i][j-1]+a[i-1][j]-a[i-1][j-1];
            cout<<a[i][j]<<" ";
        }
        cout<<endl;   
    }
    return 0;
}